Função Exponencial - Gráfico.

-

Gráfico da Função Exponencial

A função exponencial pode ser representada através de um gráfico traçado a partir de pontos no plano cartesiano. Como nesse tipo de função a base é maior que 0, a imagem será positiva e não existirão pontos nos quadrantes III e IV - que caracterizam uma imagem negativa. 

Este gráfico sempre estará abaixo do eixo x no plano cartesiano. Deste modo, quando a função é decrescente, os valores de y aproximam-se de zero na medida que o valor de x cresce. Já na função crescente, se x cresce y também cresce. 

Para construir o gráfico da função é necessário atribuir valores para x e montar uma tabela com os respectivos valores de f(x), marcando os pontos no plano cartesiano e, por fim, traçar a curva do gráfico. 

Observe abaixo os gráficos das funções crescente e decrescente: 

Como construir o gráfico de uma Função Exponencial?
Em uma função qualquer, encontrar pares ordenados que pertençam ao seu gráfico é tarefa simples: basta escolher valores para x e encontrar os valores de f(x) ligados a eles no contradomínio. Isso é feito substituindo o valor de x escolhido na função e calculando a expressão numérica resultante.

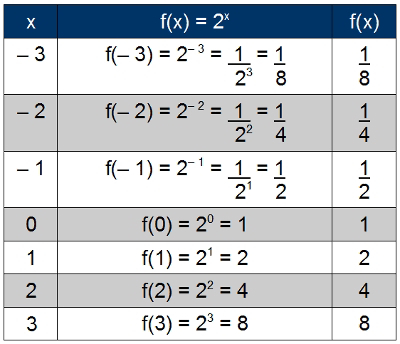
1º Exemplo: para encontrar 5 pares ordenados pertencentes ao gráfico da função f(x) = 2x, usaremos os valores x = – 3, x = – 2, x = – 1, x = 0, x = 1, x = 2 e x = 3 e preencheremos a seguinte tabela:

Com a tabela preenchida, perceba que cada valor de x se relaciona a um valor de f(x) que pode ser compreendido como y no par ordenado. Sendo assim, os pares ordenados formados são:


A = (– 3, 1/8)

B = (– 2, 1/4)

C = (– 1, 1/2)

D = (0, 1)

E = (1, 2)

F = (2, 4)

G = (3, 8)

Para desenhar o gráfico, marque os pontos acima do plano cartesiano e desenhe uma curva que os contenha. Atenção: os pontos não devem ser ligados com linhas retas, devem estar sobre uma curva.


2° Exemplo: Fazendo os mesmos procedimentos para a função f(x) = 0,25x, obtemos os seguintes pontos:

A1 = (– 3, 64)

B1 = (– 2, 16)

C1 = (– 1, 4)

D1 = (0, 1)

E1 = (1, 1/4)

F1 = (2, 1/16)

G1 = (3, 1/64)

Construímos o gráfico dessa função junto ao gráfico do primeiro exemplo para comparação:


Vamos aos exercícios!

1. Esboce o gráfico das funções definidas a seguir.

a) f(x) = 3ˣ

b) g(x) = (1/3)ˣ

Se não conseguiu responder a questão, basta acessar o link do vídeo abaixo.


Referências:



Comentários

Postar um comentário

Postagens mais visitadas deste blog

Noções das Teoria dos Conjuntos - Descrição por uma Propriedade

-
Imagem
DESCRIÇÃO POR UMA PROPRIEDADE Quando queremos descrever um conjunto A por meio de uma propriedade característica P de seus elementos x, escrevemos: 𝐴 = {𝑥 ; 𝑥 tem a propriedade 𝑃} e lemos: “A é o conjunto dos elementos 𝑥 tal que 𝑥 tem a propriedade 𝑃”.  Exemplos: 1º) {𝑥 ; 𝑥 é estado da região Sul do Brasil} é uma maneira de indicar o conjunto: {Paraná, Santa Catarina, Rio Grande do Sul}  2º) {𝑥 ; 𝑥 é divisor inteiro de 3} é uma maneira de indicar o conjunto: {1, −1, 3, −3} 3º) {𝑥 ; 𝑥 é inteiro e 0 ≤ 𝑥 ≤ 500+ pode também ser indicado por: {0, 1, 2, 3, … , 500} Vamos aos exercícios! ° Descreva por meio de uma propriedade dos elementos. a)A={+1, -1, +2, -2, +3,-3, +6, -6}  b) B={-10,-20,-30,-40} c) C={1, 4, 9, 16, 25, 36, . . .}  Respostas a)A={+1, -1, +2, -2, +3,-3, +6, -6} ( A únicas características que podemos analisar dentro do conjunto é que todo elemento possuí seu simétrico dentro do conjunto). Sendo assim: R=x é simétrico de x. b) B={-10,-20,-30,-40} ( A característi
Leia mais

Conjuntos Numéricos - Conjunto dos Números Reais.

-
Imagem
Conjunto dos números Reais Números Irracionais Existem números cuja representação decimal com infinitas casas decimais não é periódica. Por exemplo, o numeral decimal 0,1010010001... (em que o número de algarismos 0 0 intercalados entre os algarismos 1 vai crescendo) é não periódico. .  Ele representa um número não racional. Ele representa um número irracional. Outros exemplos de números irracionais: 1,234567891011  6,202002000 …  34,56789101112 … Chama-se conjunto dos números reais — símbolo ℝ — aquele formado por todos os números com representação decimal, isto é, as decimais exatas ou periódicas (que são números racionais) e as decimais não exatas e não periódicas (que são números irracionais). Dessa forma, todo número racional é número real, ou seja: ℚ  ⊂  ℝ  Além dos racionais, estão em ℝ números irracionais como: √ 2 = 1,4142136 … 𝜋 = 3,1415926 … Se quisermos outros números irracionais, poderemos obtê-los, por exemplo, por meio da expressão 𝑝, em que  √ 𝑝 é primo e positivo. 
Leia mais

Função Definida por mais de uma sentença - Gráfico.

-
Imagem
Função definida por mais de uma sentença - Gráfico Para construir o gráfico de uma função definida por mais de uma sentença, devemos  fazê-lo por partes, considerando a lei de formação que determina cada uma das partes  da função. Por exemplo, vamos construir o gráfico da função g: R→R, definida por: Vamos construir separadamente o gráfico correspondente a cada sentença da função e depois reunir essas representações no mesmo plano cartesiano. I. Considerando a sentença g¹(x) = x + 3, se x  ≤  2. O gráfico correspondente é o gráfico da função afim definida por y = x + 3, em que x  ≤  2 Nesse caso, escolhemos dois valores de x pertencentes intervalo indicado e determinamos dois pontos pertencentes à reta correspondente a esse gráfico. II. Considerando a sentença g²(x) = x _ 1 se 2 , x < 5. O gráfico correspondente é o gráfico da função afim definida por y = x _ 1, em que  x  ∈  ]2, 5]. Nesse caso, escolhemos dois valores de x  ∈  ]2, 5] e determi
Leia mais